Inspiration4Learning

Verspreiding van een virus

We beschrijven hier enkele ideeën om covid-19 in de rekenles te bespreken. We beperken ons tot enkele simpele spelletjes om basisideeën aan de orde te stellen.

Lesgeven met een applet over het verspreiden van een virus

De NCTM -- een Amerikaanse vereniging van wiskundeleraren -- heeft een mooie applet dat de snelheid van de verspreiding van een virus in beeld brengt. De applet is in het Engels, maar het kan je in de klas helpen om met de leerlingen de verspreiding van een virus te bespreken. Kijk eens naar de NCTM Applet over het verspreiden van een virus. Je vindt daar niet alleen de applet, maar ook een uitleg hoe de applet werkt, een uitleg over de wiskunde en een serie activiteiten voor verschillende leeftijden.

Enkele spellen voor in de klas

Zo'n applet zal niet altijd duidelijk zijn. Je voelt niet aan den lijve hoe de verspreiding precies werkt. Diverse spelletjes kunnen beter helpen om de betekenis van de R-waarde (dit geeft aan hoeveel mensen één geïnfecteerde persoon na enkele dagen gemiddeld heeft geïnfecteerd) te onderzoeken. Met zulke spelletjes kunnen leerlingen ook onderzoeken wat het effect van 'social distancing' precies is. Niet alleen de R-waarde is belangrijk. Nu is er ook nadruk op de K-waarde. Het Nemo legt uit wat de K-waarde precies is.

De spellen die hier beschreven worden helpen de leerlingen om te zien hoe we geleidelijk aan een beter model bouwen voor de verspreiding van een virus.

Tikkertje

Haast ieder kind heeft wel eens tikkertje gespeeld. Eigenlijk is tikkertje een speciaal geval van virus verspreiding. Je geeft de beurt (het virus) door aan één andere persoon en jij bent er van af (genezen). In dit model is het wel zo dat je weer getikt kan worden (opnieuw besmet kan worden). Bij een echt virus hopen we dat de meeste mensen niet opnieuw worden besmet. Dit spel blijft maar door gaan. Je kan een variant introduceren: als je iemand hebt getikt, dan mag je even aan de kant zitten. Geleidelijk aan wordt de groep spelende kinderen (nog niet besmet) kleiner en kleiner. Bij deze variant op tikkertje kan je onder meer met de kinderen bespreken hoeveel ronden nodig zijn tot dat iedereen de beurt heeft gehad.

Tikkertje is een spel met een R-waarde van 1: één besmet persoon besmet ook weer één persoon. Het is niet zo geschikt als model voor het verspreiden van een virus. De leerlingen zullen zeker kunnen beschrijven waarom dit niet lijkt op de verspreiding van een virus. Iemand die ziek is maakt meer mensen ziek, je bent niet zo snel genezen, soms wordt je opnieuw ziek, mensen kunnen in kleinere groepen leven,... Andere spellen helpen om een beter model te ontwikkelen.

Het ga-staan-spel

Nieuwe spelregels

Door de spelregels te veranderen, kunnen we andere R-waarden bekijken. Dit gebeurt al met het ga-staan-spel. De regels van dit spel zijn:

1. Als we beginnen zit iedereen
2. Jij vraagt een leerling om op te staan
3. Deze leerling vraagt vervolgens 2 andere leerlingen om op te staan
4. Die leerlingen vragen ieder aan twee andere leerlingen om op te staan
5. Etc

Dat gaat opeens heel wat sneller. Nadat je dit een of meer keer hebt gespeeld, kan je een aantal vragen stellen, bijvoorbeeld:

• Na hoeveel ronden iedereen staat?
• Waarom is dat zoveel sneller dan met tikkertje?
• Hoeveel ronden zullen nodig zijn om de hele school te besmetten (dat wil zeggen te laten staan?)
• Na hoeveel ronden zal de hele stad/dorp besmet zijn?
• Wat verandert er als we niet 2 mensen aanwijzen, maar steeds 3 mensen aanwijzen?

Laat de klas deze variant enkele keren spelen.

De verspreiding representeren op het bord

Je kunt overwegen om samen met de leerlingen een van de ronden op het bord na te tekenen. Deze boom geeft een idee van hoe zo'n representatie er uit kan zien.

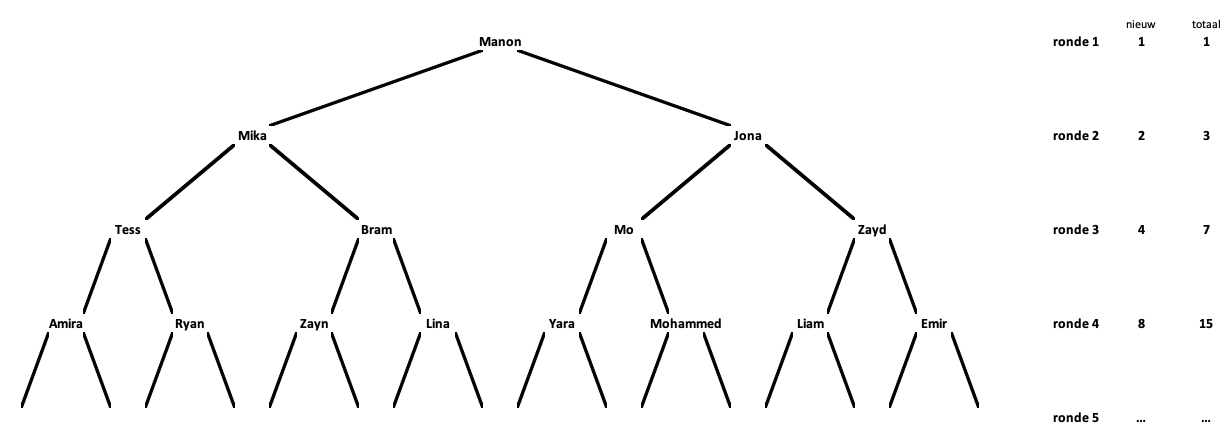
Een R-waarde van 2 en exponentiële groei

De R-waarde van dit spel is 2. Een besmet persoon infecteert steeds 2 andere mensen. De groei is exponentieel. De leerlingen kunnen met dit spel gaan zien hoe snel dat gaat. De hele school of de hele stad is veel sneller besmet dan de meeste leerlingen maar verwachten. Het is belangrijk dat ze in de gaten krijgen dat een exponentiële groei zo overweldigend is.

De leerlingen kunnen met elkaar in de groepjes bespreken hoeveel mensen nieuw geïnfecteerd worden in ronde 5, 6, 7... en hoeveel totaal geïnfecteerden er zijn na iedere nieuwe ronde. Zie je de regelmaat in de aantallen nieuwe infecties (machten van 2) en het totaal aantal geïnfecteerden (machten van 2 min 1). Het is mooi om de leerlingen vervolgens in een groepje te laten nadenken hoe een boom er uitziet als ze iedere keer 3 mensen aanwijzen.

Het spel met twee-kleurige fiches

Dit spel en de volgende spellen kun je ook door leerlingen in groepjes laten spelen. De leerlingen hebben dan een groot aantal twee-kleurige fiches nodig. Zeg dat de fiches aan een kant blauw en aan de andere kant geel zijn. Dan is de spelregel dat ze beginnen met alle gele kanten boven. Vervolgens draaien ze een fiche om, en met iedere ronde draaien ze twee andere fiches om etc. In het begin is dit verwarrend voor leerlingen, daarom is het waarschijnlijk verstandig het eerst met de hele klas te spelen als een ga-staan-spel en daarna pas in de groepjes met de fiches.

Het ga-staan-spel met kans

In werkelijkheid leidt niet ieder contact tot het verspreiden van een virus. Dit kunnen we in het spel inbouwen. Daartoe veranderen we de spelregels een beetje. We laten het aantal mensen dat je kunt besmetten afhangen van de worp van een munt of dobbelsteen.

Met het opgooien van een munt

De spelregel is nu: "Je wijst niet altijd 2 andere leerlingen aan, maar gooit eerst een munt op. Bij kop wijs je één andere leerling aan om op te staan. Bij munt wijs je 2 andere leerlingen aan om op te staan, etc".

Laat de leerlingen eerst in kleine groepjes bespreken wat ze denken dat er nu zal gaan gebeuren. Terwijl je rondloopt en naar de groepjes luistert, kan je aan de volgende vragen denken:

• Na hoeveel ronden denk je dat iedereen in de klas staat?
• Gaat dit ook sneller dan met tikkertje? Waarom wel/niet?
• Gaat het sneller dan het ga-staan-spel? Waarom wel/net?

Laat de klas deze variant enkele keren spelen. Je kunt overwegen om van een van de ronden een boom te tekenen.

We kunnen bij spel ook de R-waarde berekenen. Deze heeft te maken met de kans dat je iemand besmet. In de helft van de gevallen besmet je 1 persoon, in de helft van de gevallen besmet je 2 personen.

Met een dobbelsteen

Deze keer gooit een leerling een dobbelsteen. Is de waarde op de steen 1,2, of 3 dan infecteert de leerling niemand. Is de waarde 4 of 5 dan infecteert de leerling één andere leerling. Is de waarde 6 dan infecteert de leerling 3 leerlingen.

Laat de leerlingen het spel een paar keer spelen. Wat opvalt is dat dit keer de infectie steeds uitdooft. Soms heel snel, met een worp is het over. Soms duurt het iets langer, maar waarschijnlijk zal nooit de hele klas geïnfecteerd raken. Wacht tot leerlingen dit gaan opmerken. Dat is een goed moment om ze te vragen wat nu het verschil is tussen de laatste drie spellen.

In deze spellen simuleren we verschillende R-waarden. Met wat kennis over kansen, is deze R-waarde te berekenen.

Ogen op de dobbelsteen	1	2	3	4	5	6
Aantal personen besmet	0	0	0	1	1	3

Als het aantal besmettingen volgens deze tabel wordt bepaald, dan is de R-waarde 0×⅙ + 0×⅙ + 0×⅙ + 1×⅙ + 1×⅙ + 3×⅙, oftewel ⅚. Dat betekent dat bij de meeste simulaties het aantal besmettingen zal uitdoven. In de klas zal je zien dat bij sommige groepen de besmettingen snel uitdoven, bij andere groepen kan het iets meer tijd in beslag nemen.

Bespreek vervolgens met de leerlingen wat je aan waarden kan veranderen om te zorgen dat het aantal besmettingen steeds groter wordt. Om bijvoorbeeld een R-waarde van 1⅓ te creëren kunnen we de tabel veranderen in:

Ogen op de dobbelsteen	1	2	3	4	5	6
Aantal personen besmet	0	0	0	1	1	6

De R-waarde is nu immers 0×⅙ + 0×⅙ + 0×⅙ + 1×⅙ + 1×⅙ + 6×⅙. Als kinderen met deze tabel de simulatie spellen dan zal bij sommige groepen de besmetting uitdoven terwijl bij andere groepen het snel groter wordt.

Het ga-staan-spel met een social distancing

Het idee van social distancing is dat we minder contacten hebben en daarom -- als we geïnfecteerd zijn -- minder mensen zullen besmetten. Daarom organiseren sommige sporten kleine bubbels waarin wordt afgesproken dat men alleen contact zal hebben met de mensen in de bubbel. We gaan dit in de klas naspelen. We veranderen de spelregels nog een keer. Als jij andere mag aanwijzen, dan gooi je eerst met een munt. Bij kop wijs je één andere leerling in je groepje aan om op te staan. Bij munt wijs je 2 andere leerlingen in jouw groepje aan om op te staan, etc".

Laat de leerlingen eerst in kleine groepjes bespreken wat ze denken dat er nu zal gaan gebeuren. Terwijl je rondloopt en naar de groepjes luistert, kan je aan de volgende vragen denken:

• Na hoeveel ronden denk je dat iedereen in de klas staat?
• Gaat dit ook sneller dan met tikkertje? Waarom wel/niet?
• Als we lang doorspelen, komt er dan een moment waarop iedereen in de klas staat? Waarom wel/net?

Laat de klas deze variant enkele keren spelen.

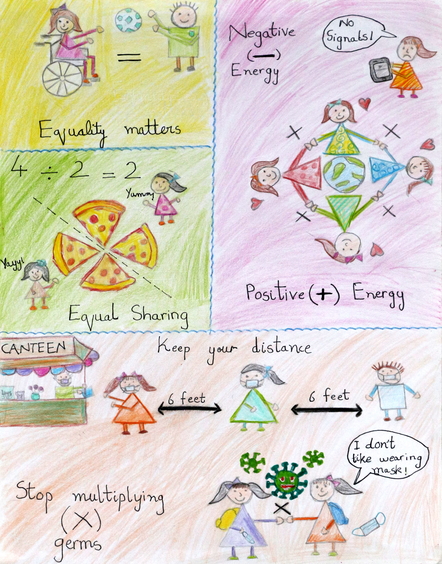
Posters over Covid gemaakt door leerlingen

De IDM 2021 heeft ook enkele mooie posters over Covid en wiskunde opgeleverd. Op hun website zien je ook andere posters te bekijken en is te lezen wie de makers zijn en wat ze bij de poster dachten.