|
Inspiration4Learning |
Rekenen op de rand van de krant
Er gebeurt altijd veel in het nieuws. Zo nu en dan geven nieuwsmedia allerlei feiten wiskundige minder correct door. Op andere momenten vormt een foto of tekst een mooie aanleiding voor wat wiskunde. Het leek ons aardig enkele hier op te nemen. Het is rekenen op de rand van de krant, dat wil zeggen dat de leerlingen aan de hand van een recente gebeurtenis een nieuwsbericht controleren of naar aanleiding van zo'n nieuwsbericht verder denken. Met een klik op een onderwerp klap je het uit en weer in. Vertel wat er in de klas gebeurde nadat je iets uitprobeerde. Zie je ook een mooie rekenaanleiding in de krant, stuur het me toe.

|
De afgelopen tijd heeft men in de Keukenhof 7 miljoen bloembollen geplant. Op veel plekken zitter er drie bollen vlak naast elkaar in de grond. Die bollen komen op verschillende moment uit, hierdoor is het bloembed voortdurend gevuld en is de tuin mooi. Voorjaarsbloeiende bloembollen worden na de groei (rond juni) gerooid, gedroogd en opgeslagen. In oktober of november worden ze weer geplant. Als je 7 miljoen bollen wilt opslaan, wat voor ruimte heb je dan nodig: een doos, een klaslokaal, het schoolgebouw, een schuur ter grootte van een voetbalveld? Het stapelen van doosjes is makkelijker dan het stapelen van bollen. Een deel van de leerlingen zal vermoedelijk kleine doosjes gaan stapelen. Ze moeten dan bedenken wat er gebeurt als je meer doosjes in de lengte, breedte en hoogte vergroot, zeg dat je tien keer zoveel doosjes in de lengte, breedte en hoogte legt. Het aantal dozen wordt dan 1.000 keer groter. Zeven ruimten van 100 bij 100 bij 100 bollen is al 7 miljoen bloembollen. Als een gemiddelde bol een diameter van 5 cm heeft, dan heb je dus 7 ruimte van 5 bij 5 bij 5 meter nodig. Een klas lokaal is vaak 7 bij 7 meter en zeg 2,5 meter hoog. Dat is ongeveer de zelfde inhoud als een ruimte van 5 bij 5 bij 5. Dus 7 volle klaslokalen is ongeveer genoeg. Wel moet je ieder lokaal tot de nok toe vullen. Andere groepen leerlingen pakken het waarschijnlijk anders aan. Mogelijk hebben ze doosjes met 10 of 100 bollen in een tuincentrum gezien en gaan ze daarmee aan de slag. Dat is geen probleem. Zij zullen ook het aantal dozen in een lokaal bepalen of ze zullen nagaan hoe groot de ruimte moet zijn om er een groot aantal dozen in op te slaan. 
Bij het rooien worden bollen vaak gezift (gesorteerd op grootte). Wat gebeurt er als de bolomvang verdubbelt? De vergrotingsvraag zal nu voor alle leerlingen terugkomen. Heb je nu het dubbele aantal lokalen nodig of heb je veel meer lokalen nodig? Hoeveel precies? Bij een vergrotingsfactor 2, zal de inhoud met een factor 8 (23) groeien. Vertel dit niet, maar geef de leerlingen voldoende tijd om dit zelf uit te zoeken. De vergrotingsvraag komt ook terug bij de kopieermachine. Ik wil een A4 vergroten naar een A3, wat moet ik dan instellen? Of ik wil een A3 verkleinen naar een A4. Waar komen die getallen precies vandaan? Er zijn natuurlijk veel meer bolvormige objecten die op grootte worden gesorteerd. Denk bijvoorbeeld aan uien en aardappelen, maar ook oesters worden op grootte gesorteerd en benoemd. 
Over bloembollen heeft Webkwestie heeft een opdracht ontwikkeld. Hieronder onderzoeken leerlingen hoe een bol in elkaar zit, hoe je bol plant en hoe je een bloembol moeten verzorgen. |


|
Een dijk rond een reservoir met afvalwater staat op het punt van doorbreken. Men probeert met pompen het reservoir op tijd leeg te pompen. In het bericht meldt NOS nieuws dat het reservoir ruim 2 miljard liter water bevat. Men pompt duizenden liter water per minuut weg en heeft 10 tot 12 dagen nodig om het reservoir leeg te pompen. Twee miljard liter water in 10 dagen verplaatsen. Hoeveel liter moet je dan per minuut wegpompen? Met een aantal pompen kan je al gauw heel wat water verplaatsen. Een kleine pomp kan al 60.000 liter per uur verplaatsten; groter pompen kunnen 3.000 m3 of meer per uur verplaatsen. Hoeveel pompen heb je nodig om dit in 10 dagen te doen? De New York Times geeft meer informatie. Het reservoir bevat ongeveer 400 miljoen gallon afvalwater. Tussen de 2 en 3 miljoen gallon water lekt per dag uit het reservoir. Op 26 maart bevatten het reservoir 480 miljoen liter, op 3 april bevatte het 390 miljoen liter. Nu wordt 22.000 gallon per minuut overgepompt. Kloppen de getallen die de NOS in het bericht heeft opgenomen? Dit probleem vraagt om handig rekenen. Dat kan je natuurlijk met een rekenmachine doen, maar ook met benaderd rekenen. Als je het gaat benaderen, dan moet je de getallen goed kiezen. Een dag is 24 uur, maar het rekent weel handiger met 25 uur. Een dag is 24 × 60 minuten; maar het rekent makkelijker als je het aantal minuten in een dag met 25 × 60 minuten benadert, dus ongeveer 1.500 minuten. Schattend rekenend lijkt dit probleem op de vraag wie in onderstaande tekening een miljard seconden oud is. 
Verjaardagen zijn altijd leuk; maar je kan in de klas bijzondere verjaardagen en bijzondere lengten vieren. Wij zijn een groot voorstander van de 1-meter dag? Laat leerlingen in de gaten houden wanneer ze je 1 meter lang zijn? Die dag is moeilijk te voorspellen. Maar het 500 of 1000 wekenfeest, het 3.000 dagen feest, of het 1 miljard seconden feest is precies te bepalen. Laat leerlingen een eigen lijst maken van bijzondere dagen in hun leven en samen een klassenlijst maken. Zo kunnen ze elkaar's rekenwerk controleren. Het 1000 wekenfeest van de leerlingen kan niet te ver uit elkaar liggen, en het verschil in leeftijd (geboortedag) zegt iets over het verschil in tussen de momenten waarop het 1000 wekenfeest gevierd kan worden. Kunnen ze een mooi feest bedenken voor familieleden? |

|
"De politie wil over vijf jaar 35 procent agenten met migratie achtergrond" melden diverse media. Het artikel van NOS nieuws meldt ook dat de komende vijf jaar zeker 17.000 van de 63.000 agenten met pensioen gaan. Kan de politie dan in vijf jaar deze 35% norm eigenlijk halen? Het is een mooie vraag om de kinderen aan te laten puzzelen. Er zijn verschillende manieren om hier tegen aan te kijken. Vijfendertig procent van 63.000 is net iets meer dan 22.000. Dat zou dus alleen kunnen als er nu al 5 duizend agenten met een niet-westerse achtergrond bij de politie werken en alle nieuw aangenomen agenten (17.000) een niet-westerse achtergrond hebben. Als 50% van de nieuwe aanwinst een niet-westerse achtergrond hebben (8.500 agenten), dan moeten er nu in ieder geval 13.500 agenten een niet-westerse achtergrond hebben (en niet vertrekken). Het komt dus deels neer op het maken van enkele reële aannamen. Want wie er precies vertrekt en wie zal worden aangenomen weten we niet. Leerlingen zullen waarschijnlijk zich ook afvragen hoeveel agenten met een niet-westerse achtergrond nu al in dienst zijn. Het stellen van goede vragen en het verhelderen van je aannamen is heel belangrijk. Antwoord op die laatste vraag kunnen ze mogelijk op internet vinden. Op 12 juni 2020 meldde de Volkskrant dat 7 procent een niet-westerse achtergrond heeft: "Van de politiemedewerkers – van schoonmaker tot korpschef – heeft 7 procent een niet-westerse migratieachtergrond, daarmee worden personen bedoeld ‘met als migratieachtergrond een van de landen in Afrika, Latijns-Amerika en Azië (exclusief Indonesië en Japan) of Turkije’." Laten we aannemen dat de cijfers van de Volkskrant juist zijn. 7% van 63.000 medewerkers is 4.410 medewerkers. Als alle nieuw aangenomen agenten een niet-westerse achtergrond hebben, dan zijn er in totaal 21410, dus net geen 34%, agenten met een niet-westerse achtergrond. Dat gaat zo nooit lukken. Het lijkt me onmogelijk om de komende vijf jaar alleen agenten met een niet-westerse achtergrond aan te nemen. Ten eerste is het de vraag of er zoveel kandidaten zijn, maar ook zo sterk discrimineren in het selectieproces gaat vermoedelijk grote weerstand oproepen. Willen ze de 35% halen dan zouden ze het aantal agenten drastisch moeten verhogen. Ook hier kan je aan rekenen. Om het percentage van 7% naar 35% te brengen, zul je in ieder geval meer dan 35% agenten met een niet-westerse achtergrond aannemen. Zouden de leerlingen deze redenering maken en aan elkaar uitleggen? Zeg 50% van alle nieuwe agenten heeft een niet-westerse achtergrond. Hoe groot moet de politie dan worden om die 35% te halen? Wanneer je dat doorrekent dan zul je zien dat het aantal politiemedewerkers nagenoeg moet verdubbelen om dat percentage van 35% te halen. Het blijkt dus een leuke maar onhaalbare uitspraak te zijn. Geef de leerlingen alleen de gegevens en vraag of dit de politie gaat lukken. Laat de leerlingen zelf bepalen hoe ze dit gaan bepalen en hoe ze hun klasgenoten gaan overtuigen. |

|
Het NOS nieuws kopt met: 7684 nieuwe besmettingen, stijging vlakt iets af". Wat bedoelen ze dan? Is het aantal besmettingen nu toegenomen of afgenomen? Regelmatig wordt in een krant zo'n soort koptekst gebruikt. Eigenlijk schrijven de kranten dan over de eerste afgeleide, maar de meeste lezers begrijpen dat helemaal niet. Vraag de leerlingen om een grafiek te maken dat hier bij zou kunnen horen en laat ze uitleggen waarom die grafiek weergeeft wat de krant zegt? Laat ze ook uitleggen wat nu toeneemt en wat afneemt. Ergens in dat gesprek zullen de leerlingen wel over de toename per dag gaan praten en kunnen ze laten zien dat die toename kleiner wordt. Het aantal stijgt, maar de toename in het aantal daalt. Dat is interessant. Zouden ze een grafiek van de toename kunnen tekenen? Natuurlijk zijn er ook andere berichten met vergelijkbare kopteksten: Stijging van huizenprijzen neemt af, Stijging benodigde ambulances neemt af, Stijging consumentenprijzen daalt van 2,7 naar 1,8 procent, Stijging aantal WW-uitkeringen neemt af. Hier zijn twee vergelijkbare berichten over de vleesproductie en het aantal incidenten waarbij door een stopsein wordt gereden.
|

|
Ontbossing is een ernstig probleem dat wereldwijd diversiteit van diersoorten, het klimaat en het ecosysteem in gevaar brengt. In 2020 is de ontbossing weer toegenomen. De NOS meldt dat in 2020 een oppervlakte van 42.000 vierkante kilometer (de grootte van Nederland) aan oerbossen is gekapt. Dat spreekt wel aan. Hoeveel bomen zouden in Nederland passen als we alle huizen, wegen, pleinen, scholen platmaken en vervangen door bomen? Hoeveel bomen in oerbossen zijn er afgelopen jaar gekapt? Nu is het aantal bomen dat op 42.000 vierkante kilometer past afhankelijk van de boomdichtheid. Deze is niet overal gelijk. Dat blijkt ook uit de figuren c en d (hieronder) uit het artikel van Hoang, N.T., en Kanemoto, K. (Mapping the deforestation footprint of nations reveals growing threat to tropical forests. Nat Ecol Evol (2021).) Het aantal bomen dat per hoofd van de bevolking verloren ging is het grootst in Zweden, maar het aantal verloren vierkante meter bos is het grootst in Canada. Ik zou alleen de twee grafieken aan de leerlingen geven en ze vragen om uit te leggen hoe dit precies zit. Er valt wel een vergelijking te trekken over de dichtheid van de bossen in Zweden en Canada. Moet je daar trouwens het aantal inwoners en de grootte van het land voor weten of kan je daar aan rekenen zonder die aantallen te kennen? 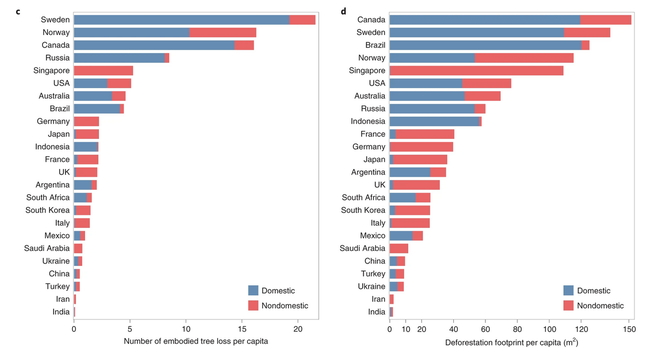
|
Het NK tegelwippen is begonnen. dit kampioenschap loopt van 29 maart tot 30 september 2021. Het is goed voor de natuur, het klimaat en het lichaam. Men vergeet altijd dat het ook goed is voor het rekenonderwijs. Er valt weer veel te schatten, te berekenen, te meten. Een van de doelen is dat er miljoenen tegels gewipt wordt en vervangen wordt door planten. Laten we even uitgaan van een miljoen tegels. Hoe groot is een gebied met een miljoen tegels? Eerst even schatten: is dat een klaslokaal, het plein bij de de school, voetbalveld, de hele gemeente, heel Nederland? Dan rekenen: wat is een miljoen tegels, oeps, wat is eigenlijk de maat van een tegel. Dat kunnen de kinderen natuurlijk op het schoolplein opmeten. Wat meten ze eigenlijk: de maat van een tegel, of direct de maat van een vierkant van 10 bij 10 tegels...? Nu kunnen we eindelijk gaan rekenen. Hebben ze in de gaten dat een vierkant van 10 bij 10 tegels 100 tegels bevat en een vierkant van 100 bij 100 10.000 tegels bevat. Tussendoor kunnen we als daar bij de leerlingen behoefte aan is ook een notatie met machten van 10 introduceren. 100 schrijft men ook als 102 en 10.000 schrijft men ook als 104. Dit leidt dan weer tot de vraag wat 100 × 104?
De tegelstand geeft per gemeente de TPI (tegel per inwoner) en het aantal gewipte tegels aan. Dit vraagt toch om rekenen met verhoudingen. Hoe berekent men de TPI precies? Hoeveel inwoners denkt men dat Zwolle heeft? Zoek een plaats direct bij je school en vraag de leerlingen of de gegevens kloppen. Hoeveel tegels zou je in jouw stad moeten wippen om bovenaan te staan? Hoe groot is dat gebied?

|
Een groot schip is vastgelopen in het Suezkanaal. "Om het los te trekken, ga je eerst rekenen", zegt een directeur van Boskalis. Dat laat weer zien hoe belangrijk de wiskunde is. Voor ons is dat soort rekenen trouwens niet weggelegd. Het gaat over het drijfvermogen, over het gewicht van de olie, het gewicht van het water aan boord, het gewicht van de containers en de vracht in de containers... Maar de berichten over dit schip en de foto's die online staan geven genoeg aanleiding tot verbazing en rekenen. Het schip bevat ongeveer 20,000 containers, het is ongeveer 400 meter lang en het ligt 15 meter diep in het water. We zien niet alle containers, want een deel ligt in het ruim. Hoeveel containers zijn er ongeveer op elkaar gestapeld? Wat voor terrein heb je nodig als je die containers aan land brengt en maximaal 3 containers op elkaar stapelt? Hoe lang is een trein die al die containers vervoert?
|
In een rapportage op de radio vertelde een Belgische journalist hoe moeilijk het is om smokkel in de havens tegen te gaan: "De haven van Antwerpen is 18000 voetbalvelden groot". Wat betekent dat precies. Is de haven groter dan de bebouwde kom van Antwerpen? Wat is de oppervlakte van de haven ongeveer?
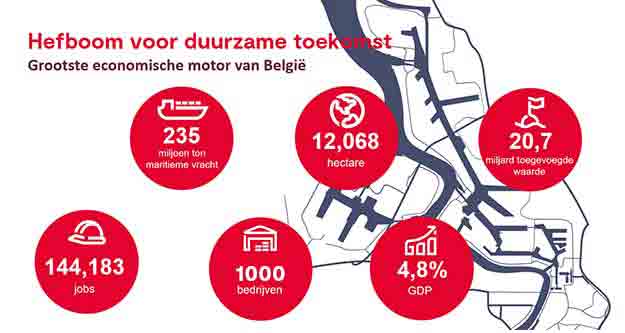
Op de website van de haven van Antwerpen staat dat de haven 11.465 hectare groot is. komt dat overeen met het idee dat de haven 16.600 voetbalvelden groot is? Rekenen ze trouwens het water mee in dit soort berekeningen of gaat het alleen over droog land?
|
|
Tel je op of vermenigvuldig je bij verhoudingen en procenten?De Verenigde Staten heeft al 44 miljoen mensen volledig gevaccineerd, melden enkele kranten. In Nederland hebben 500.000 mensen al twee prikken gehad. Waar gaat het sneller? In Groot Brittanië heeft men op een zaterdag ongeveer 900.000 mensen gevaccineerd. In Nederland werden rond die tijd gemiddeld 29.000 mensen per dag gevaccineerd. Het gaat bij al dit soort gegevens voortdurend on het verschil tussen absolute en relatieve getallen. Met andere woorden de verhoudingen vliegen ons weer om de oren. Om de lezers te helpen sneller overzicht te krijgen, publiceren veel kranten de corona cijfers als zoveel besmettingen op de honderdduizend inwoners. Gelukkig voor ons, is dat lang niet altijd het geval en zijn er genoeg artikelen die aanleiding geven om aan verhoudingen te werken. Tine Degrande (een onderzoeker uit België ) vroeg zich af waarom leerlingen bij verhoudingsproblemen soms optellen en soms vermenigvuldigen. Zij liet zien dat leerlingen een persoonlijke voorkeur voor de ene of de andere bewerking hebben. Zij gaf leerlingen onder meer het volgende probleem: Wat kan op de plaats van het vraagteken komen?:
Sommige leerlingen vulden 8 in (6+2), anderen vulden 12 in (2 x 6). In dit geval zijn beide antwoorden te verklaren. Echter deze voorkeur voor optellen of vermenigvuldigen kwam ook terug bij vragen waarbij maar een van de bewerkingen correct is. Om dat na te gaan, legde Tine de leerlingen vragen voor als:
Hierbij lieten leerlingen weer hun voorkeur voor optellen of vermenigvuldigen zien. We zien zo'n voorkeur voor een additieve of multiplicatieve benadering ook bij procenten terug. Tine concludeerde dat deze voorkeur hardnekkig is. We moeten dit in de klas dus voortdurend aan de orde stellen. Geef de leerlingen voldoende situaties waarin de ene of de andere benadering goed is en creëer een conflict met een bijbehorende discussie tussen de leerlingen over de vraag "waarom kan je hier wel optellen en niet vermenigvuldigen?" of Waarom kan je hier wel vermenigvuldigen en niet optellen?" Er zijn meer mogelijkhedenNog een opmerking. Het probleem Wat kan op de plaats van het vraagteken komen? is wiskundig gezien totaal niet interessant:
Wiskundig gezien is ieder getal goed. We kunnen bijvoorbeeld zeggen dat het punt (2,4) en het punt (6,?) op een lijn moeten liggen. Wat je ook voor het vraagteken invult, er is altijd een rechte lijn die door die twee punten gaat. Ook als we het probleem verder uitbreiden, zijn er wiskundig gezien veel meer oplossingen mogelijk. Kijk naar:
Het lijkt er op als of we overal 2 moeten bijtellen. Dat levert zeker een goede oplossing op; het vraagteken is dan 12. Vermenigvuldigen geeft zeker geen goed antwoord. Echter als we bijvoorbeeld ook aan een parabool denken, dan is meer mogelijk. Zo liggen bijvoorbeeld de punt (2,4), (6,8) en (10,44) op de parabool y= x2-7x + 14. Dus ik had ook 44 kunnen invullen. En zo zijn er — wiskundig gezien — oneindig veel antwoorden mogelijk. |
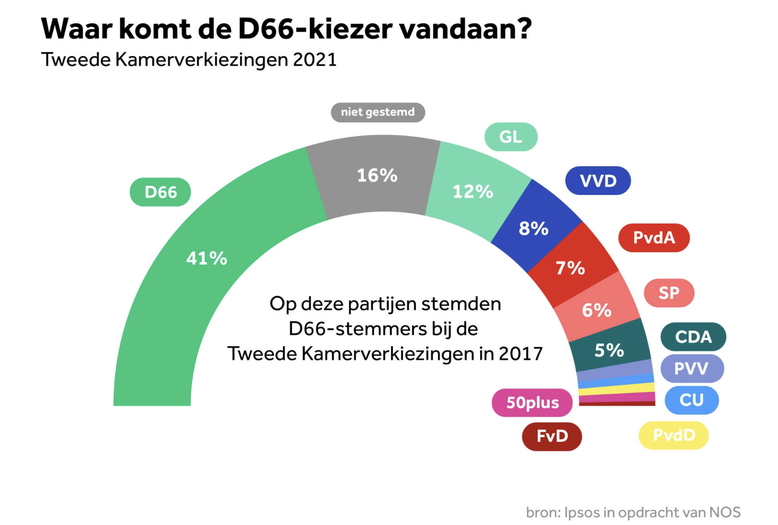
Diverse websites laten direct na de verkiezingen dit soort plaatjes zien. Ik zou mijn leerlingen hiernaar laten kijken en in kleine groepjes vragen wat ze opvalt. Ergens in de discussie zou ik laten vallen dat ik altijd dacht dat 100% een volle cirkel is. Waarom laten ze hier maar 50% zien? De advocaat van de duivel spelen is zo'n mooie rol voor een leraar.
Nadat we dit besproken hebben, laat ik ze een plaatje zien van de verkiezingsuitslag over alle partijen. Dit plaatje komt van Wikipedia en laat alleen de uitslag van 2017 zien.
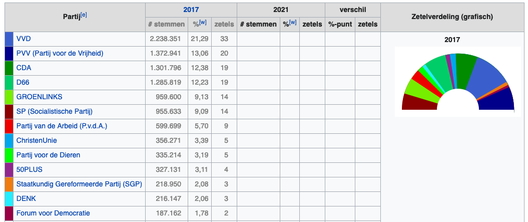
Wederom geeft de boog het totaal aantal stemmen weer. Nu kunnen we zowel het percentage stemmen als het aantal zetels per partij aangeven. Dat levert een mooie dubbele getallenlijn op.

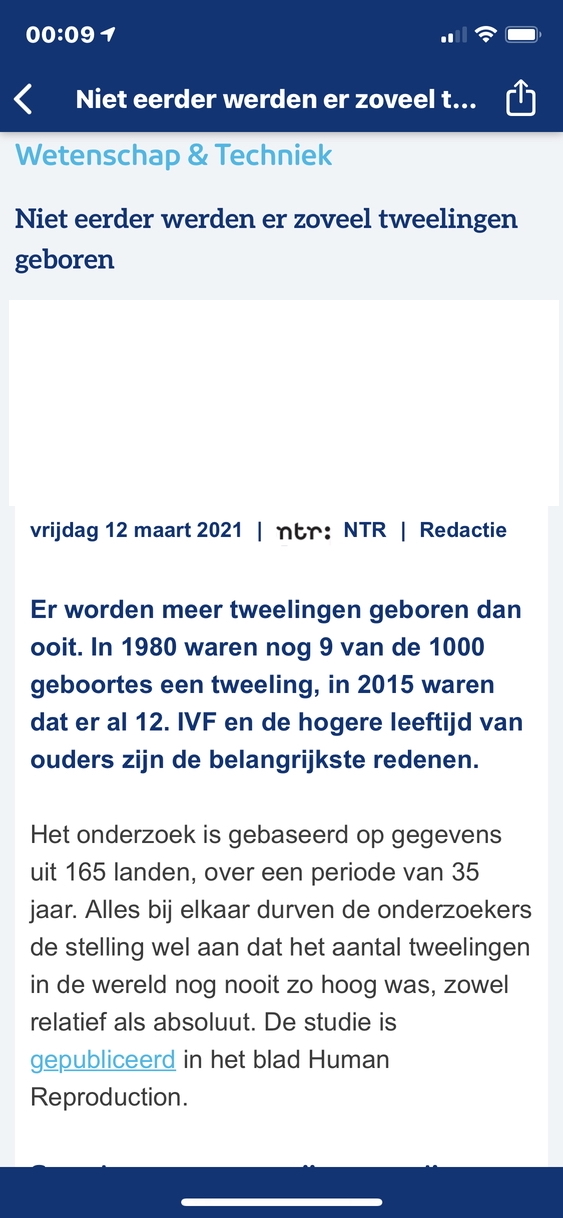
Diverse nieuwsmedia melden dat de laatste jaren meer tweelingen zijn geboren. Natuurlijk gebruikt iedere krant andere getallen in het artikel. De vraag is of die getallen echt verschillen. De NOS stelt dat er 1,6 miljoen tweelingen per jaar worden geboren. Dit bericht zegt ook dat bij 1 op de 42 geboorten sprake is van een tweeling. De NTR zegt echter dat in 2015 12 op de 1000 geboorten een tweeling is. Zou dat allemaal kunnen kloppen?
Natuurlijk betekent dit dat de leerlingen 1 op de 42 en 12 op 1000 moeten vergelijken. Maar er is ook de vraag of die 1,6 miljoen tweelingen per jaar kan kloppen. We kunnen het totaal aantal geboorten per jaar uitrekenen als we veronderstellen dat 12 op de 1000 geboorten een tweeling is en er 1,6 miljoen tweelingen zijn geboren. Maar klopt dat ongeveer met de grootte van de wereldbevolking? Hoe kan je zo'n getal controleren?
|
|
Apple is steeds actiever in de gezondheidsbranche. Nu is het mogelijk om met een applet van Apple te onderzoeken of je gehoorproblemen hebt. De meeste mensen met gehoorproblemen willen dat waarschijnlijk wel uitproberen. Ze willen meestal weten hoe ernstig het probleem is. Onlangs meldde Apple dat 1 op de 5 deelnemers in enige mate gehoorproblemen heeft. Wat betekent dit nu? Heeft 20% van de wereldbevolking gehoorproblemen? Het is altijd goed om met kinderen dit soort artikelen te bespreken. Het gaat hierbij steeds om de vraag: wat is het geheel?. Dat is altijd een belangrijke vraag en vaak letten kinderen hier niet genoeg op. Het is belangrijk bij procenten, bij breuken, bij alles. In dit geval is het verstopt in het woord "deelnemers". Mensen die gehoorproblemen ondervinden zullen eerder aan deze test meedoen dan mensen die geen gehoorproblemen ondervinden. De groep is dus geen goede afspiegeling van de hele maatschappij. Dit is ook het geval met bijvoorbeeld de Covid-19 tests. Als 11% van de onderzochte mensen positief test voor Covid-19, dan mag je niet concluderen dat 11% van de bevolking positief zal testen. De kwestie "wat is het geheel" kom je ook tegen bij beroemde vragen als:
"Wat is het geheel" is een groot idee. Je kan er in de klas nooit genoeg aandacht aan besteden. Bovenstaande vragen zijn niet de beste vragen om dit in de klas aan de orde te stellen. Het is beter om grotere problemen te zoeken waarin dit steeds aan de orde komt. |
|
|
NOS Teletekst liet dezelfde dag zien hoe de vraag wat is het geheel? in een wat complexere setting belangrijk is. Minister de Jonge vertelt dat 2/3 deel van 80 tot 85 procent van de volwassenen in juli helemaal beschermd is tegen Covid-19. Het artikel beschrijft het in enkele stappen.
Hoeveel procent van de Nederlanders is in juli helemaal beschermd? Dat levert nogal wat denkwerk op. Twee derde van 80-85 procent van de volwassenen. Hoeveel Nederlandsers zijn dat? Of hoeveel procent van de 17 miljoen Nederlanders is dat? Om deze situatie goed te doorzien, moeten de leerlingen in de gaten krijgen dat er drie verschillende gehelen in het spel zijn: alle Nederlanders (17 miljoen), alle volwassenen (14 miljoen), 80-85 procent die ingeënt wil willen (tussen de 11 en 12 miljoen). Mag je dan zeggen dat het 2/3 van 80 procent is? Mag je hier vermenigvuldigen? Waarom precies? |

De NOS meldt dat "een internationaal team van wetenschappers erin is geslaagd een ongeopende brief uit de zeventiende eeuw te lezen met behulp van scantechnologie. De brief werd gevonden in een koffer van een Haagse postmeester uit die tijd; hij kwam nooit bij de ontvanger aan". Niet alleen de NOS meldde dit. Het was wereldnieuws.
Het artikel meldt dat "de brieven niet zaten 'verpakt' in een envelop; die uitvinding volgde pas in de negentiende eeuw. Het papier was in die tijd zijn eigen envelop. Mensen bedachten allerlei manieren om het papier te vouwen. Dat had alles te maken met de inhoud: als de brief gevoelige informatie bevatte, probeerden afzenders de post goed te verzegelen zodat deze niet stiekem kon worden gelezen. Om de post op te vouwen en te verzegelen, bestonden dus talloze manieren: letterlocking genoemd. Het vouwen was even persoonlijk als een handtekening van de afzender".
Diverse websites geven informatie over het vouwen en sluiten van een brief. Op IBookBinding vind je enkele videos waarin het proces van vouwen en verzegelen wordt getoond.
Daag de kinderen uit om op een kant een verhaal te schrijven en deze zo te vouwen en met plakband dicht te maken dat andere kinderen de tekst niet kunnen lezen. Wat voor vouwen kunnen ze bedenken en hoe weten ze dat de brief dan onleesbaar is.
Met vouwen is het zelfs mogelijk een taal te ontwikkelen. De vouwen die mensen vroeger hanteerden waren erg persoonlijk. Je kon eraan herkennen wie de brief had gevouwen; het werkte dus als een soort handtekening. Ook de wijze van vouwen van de Surinaamse hoofddoeken -- de angisa -- vormt een taal. Vrouwen kunnen daardoor boodschappen en emoties uitdragen. Over taal gesproken. In Nederland hadden de molenaars een taal ontwikkeld door de wieken van de molen in een bepaalde stand te zetten.

Er doen dit jaar een record aantal partijen mee aan de Tweede Kamerverkiezingen. Hierdoor ontstaan er enkele nieuwe logistieke problemen. Foto's van die borden zijn overal te vinden. De NOS app meldt zelfs: "En dit jaar is het passen en meten op het bord, want er doen 37 partijen mee aan de Tweede Kamerverkiezingen. Ze staan er allemaal op; alle 37 precies even groot."
Maar als je de foto's bekijkt dan staan er nooit 37 partijen op. Hoe moet zo'n bord nu gevuld worden om alle 37 er op te zetten?
37 is een priemgetal. Het is niet mogelijk om het bord met bijvoorbeeld 4 rijen van 9 posters, 5 rijen van 6 posters of 3 rijen van 7 posters te vullen en dan precies 37 partijen te laten zien. De leerlingen zullen waarschijnlijk diverse vermenigvuldigingen proberen en op enig moment constateren dat 37 niet te ontbinden is. Dat is al een mooi moment om die gedachte te vieren en om dan te vragen of er meer getallen zijn die niet ontbonden kunnen worden. Of om ze uit te dagen een 'eerlijk' ontwerp voor het verkiezingsbord te maken.
Voor de IDM 2021 heeft Aubin Arroyo uit Mexico met behulp van python onderstaande poster over priemgetallen gemaakt. Zelf zegt Aubin "Deze getallen maken de wereld een betere en gelukkiger plek; je hoeft er tenminste niet om te geven als je de tafels van vermenigvuldiging op school moet leren". Op de IDM website zien je ook andere posters te bekijken en is te lezen wie de makers zijn en wat ze bij de poster dachten. Je kunt op enig moment deze poster door de leerlingen laten bespreken. Wat zien ze? Wat valt ze op? Hoe heeft Aubin geweten dat het om deze getallen gaat? Wat zou het volgende getal zijn? Hoe kun je meer getallen vinden?


De Jakarta Post had onlangs een leuke foto van kinderen die op straat de schaduw van een fiets tekenen. Die tekening is echter geen echte fiets, de verhoudingen zijn 'fout'. Is dit nu een Anamorfose? Het idee is goed te zien in de volgende schets van de firma drukwerkdeal. Je kunt een anamorfose maken door een object op een raster te tekenen en vervolgens dat raster uit te trekken.
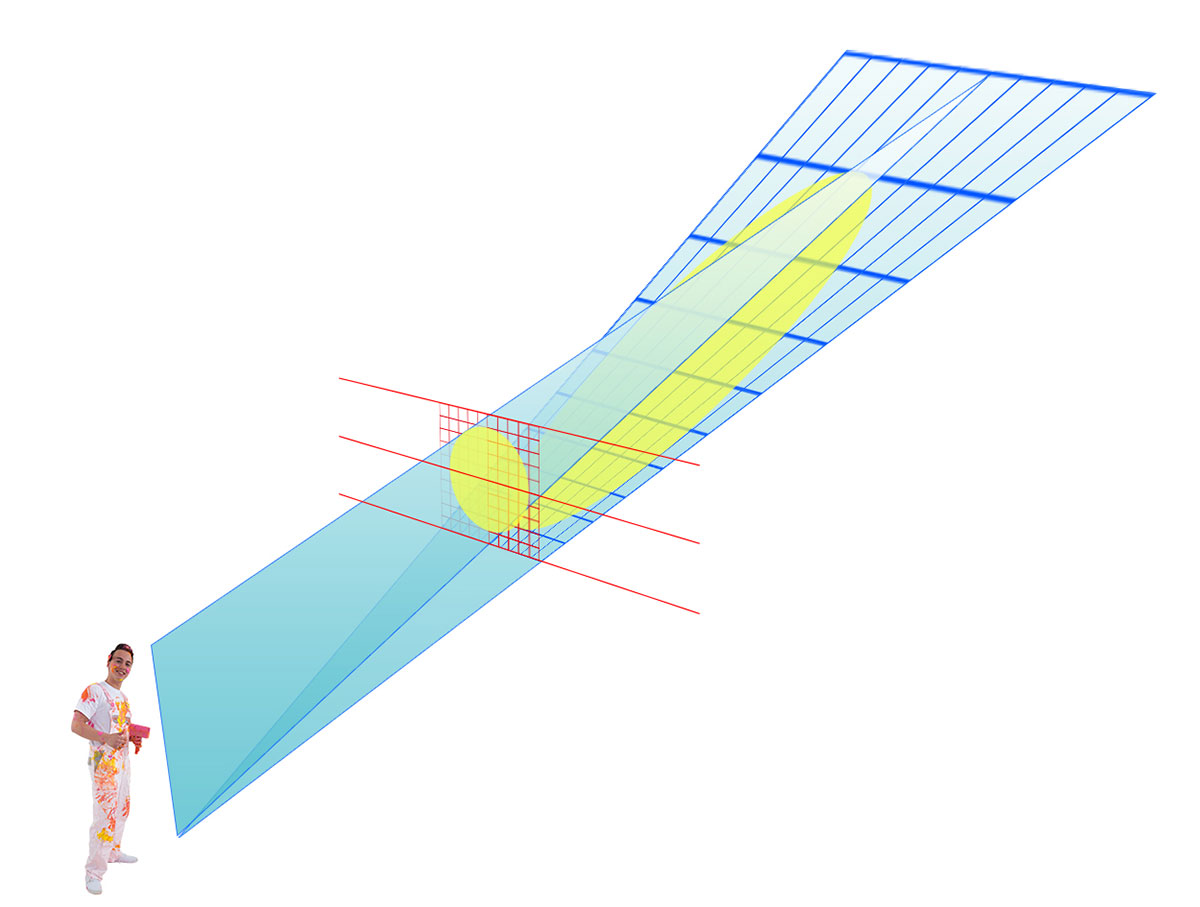
De fiets op de stoep is vanuit een heel ver standpunt (de zon) genomen. Bekijk je het van een ander standpunt dan lijkt die fiets vervormd. Dat zie je ook in de tekeningen van Julian Beever De foto van een molrat die uit de muur komt laten dat mooi zien Julian Beever.


Leerlingen kunnen heel wat kijkmeetkunde herontdekken als ze dit soort licht en schaduw activiteiten op het schoolplein gaan uitvoeren. Laat ze eens een fiets tekenen. Ze zullen gaan zien dat de getekende fiets er anders uitziet dan de echte fiets en ook dat de schaduw over tijd groter wordt. Hoe zit het met een tafelblad? Zet een tafel buiten en laat ieder uur een kind met een ander kleurtje de schaduw van het blad op de tegels tekenen. Aan het eind van de dag ga je natuurlijk met z'n alle bekijken hoe dat er uitziet. Is de grootte van het tafelblad verandert? Is het nog steeds een rechthoek? Hoe zit het met de schaduw van een tafelblad als we er in de klas met een sterke lamp op zetten? Kan ik de schaduw vervormen?
Windmolens maken al lange tijd deel uit van het Nederlandse landschap. Je ziet allerlei molens in steden en op het platteland. We gebruikten poldermolens om water te malen. We hadden industriemolens om meel te malen, hout te zagen, olie uit zaden te halen, of om bijvoorbeeld papier te maken. Tegenwoordig hebben de oude molens vooral een cultureel doel. Om energie op te wekken gebruiken we andere molens. Deze zijn hoger en slanker.
Tegen de windturbines zijn allerlei bezwaren: ze maken veel herrie, je ervaart een hinderlijke slagschaduw en trillingen, ze zijn slecht voor de volksgezondheid, ze zijn lelijk, ze belemmeren het uitzicht, de waarde van woningen in de omgeving gaat omlaag... Of deze bezwaren terecht of onterecht zijn ga ik niet beoordelen. Ik wil hier alleen kijken naar het argument dat ze zo groot zijn. Een beetje windmolen is hoog; daar vangen ze immers de meeste wind. Hoe hoog is zo'n windturbine? Of anders gezegd, hoe groot zie je een windturbine die op enige afstand van je huis wordt gebouwd?

Ik zelf woon op 50 meter van een oude molen. De stelling, dat is de omloop waar de molenaar over heen loopt, is 18 meter boven straatniveau. De vlucht van de molen, dat is de afstand van de ene wiektop tot de top van de tegenoverliggende wiek, is 25 meter. Dus het hoogste punt van de molen ligt ongeveer 43 meter boven de straat. Lijkt deze molen nu groter of kleiner dan een windturbine van 200 meter hoog die op 900 meter van mijn huis wordt gebouwd?
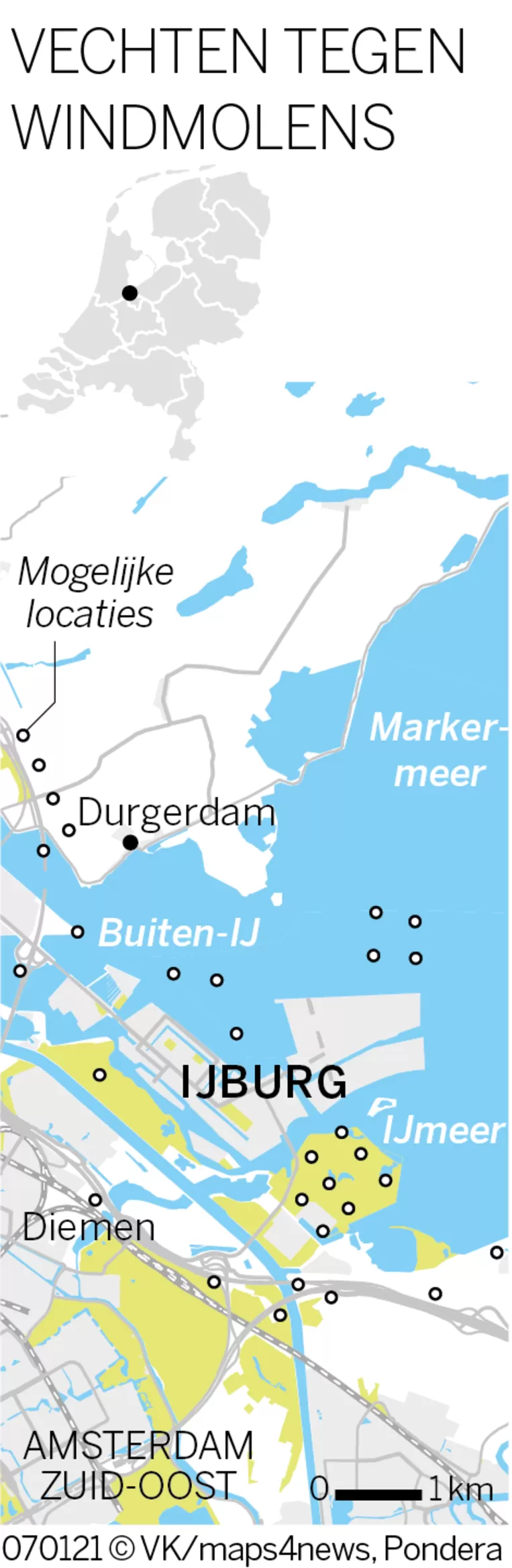
Mogelijke locaties van windmolens bij IJburg
Een plek waar de discussie over windmolens wordt gevoerd is IJburg bij Amsterdam. De Volkskrant laat een kaart zien van mogelijke plekken waar een molen kan worden geplaatst. De hoogte kan 200 meter worden. Je zou een onderzoek kunnen inleiden door te praten over de bewoners van de buurt en dat ze horizonvervuiling vrezen. De buurtbewoners willen graag begrijpen hoe groot die molens er uit zullen zien; dat wil zeggen de bewoners willen zich kunnen voorstellen hoe die molens er aan de horizon uit zullen zien als ze zelf voor hun huis staan.
Er zijn veel vragen en problemen die over kijklijnen gaan. Laat ik een andere situatie benoemen die kinderen mogelijk wel eens opgemerkt hebben of die kinderen herkennen als je het benoemt. Wanneer je op een afstand richting een stad of dorp fiets dan zie je dat ene hoge punt (kerktoren, flatgebouw, brug, molen) heel goed. Het steekt boven alle huizen uit. Maar als je in de stad (dorp) bent dan is dat hoge punt vaak niet zichtbaar. De vraag is natuurlijk hoe dat precies zit.